Heap and Trie

Heap
Heap adalah data structure yang spesial dimana ia tree-based yang treenya adalah complete binary tree.

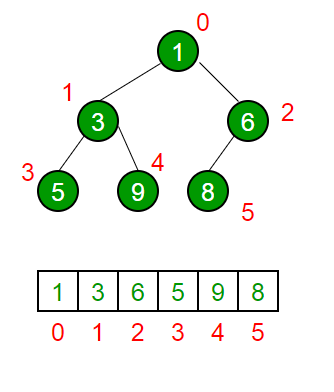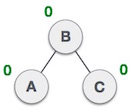
Array to Heap

Biasanya Heap dibagi menjadi dua yakni,

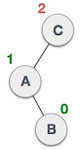
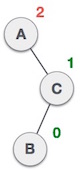
Max-Heap dan Min-Heap

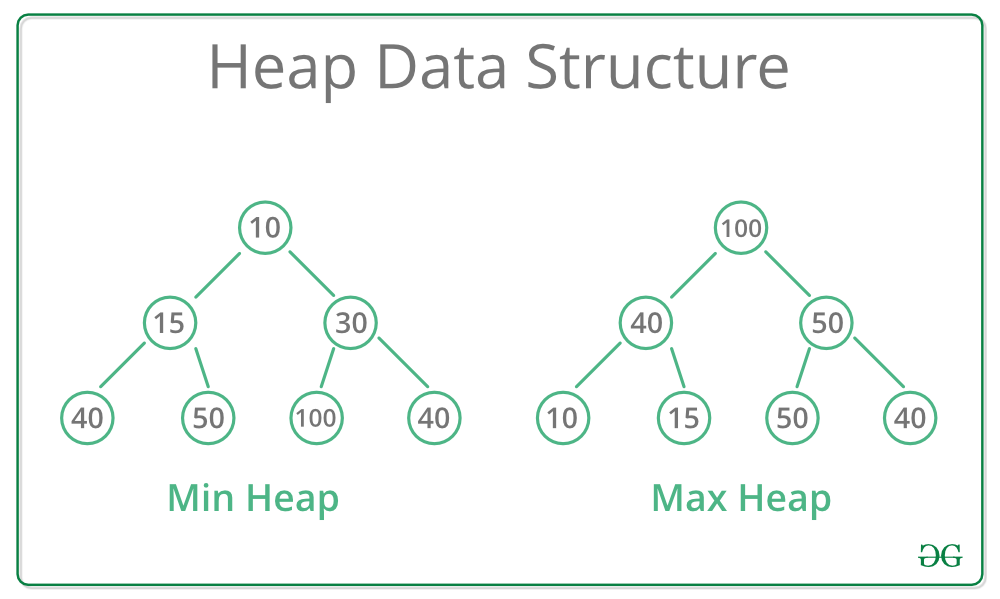Min & Max

Pada Max-Heap key pada root harus lebih besar daripada key semua childnya. Begitu juga untuk childrennya yang menjadi parent harus lebih besar daripada childrennya.

Pada Min-Heap key pada root harus lebih kecil daripada key semua childnya. Begitu juga untuk childrennya yang menjadi parent harus lebih kecil daripada childrennya.

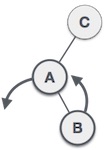
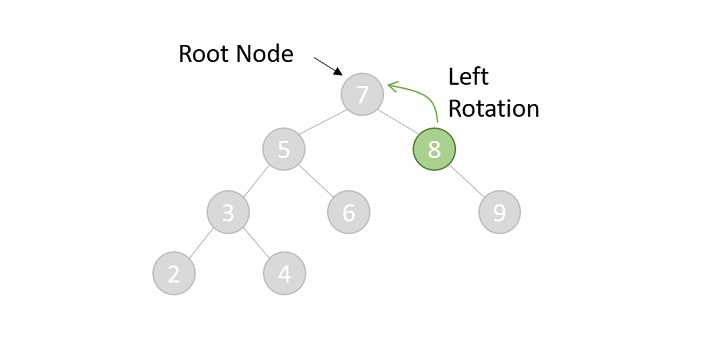
Insertion

Saat kita meng-insert data, data akan dimasukan di index terakhir pada array heap tersebut lalu data akan dibandingkan dengan parentnya, jika kondisi Min/Max Heap dilanggar maka data tersebut akan dipindahkan ke tempat parentnya (Up-Heap).

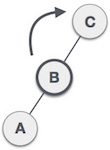
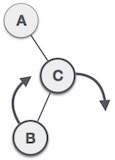
Deletion

Saat kita meng-delete data pada heap, maka root dari heap akan terhapus, lalu array heap terakhir akan langsung menggantikan root yang terdelete. Lalu data tersebut akan di bandingkan dengan childnya, jika kondisi Min/Max Heap dilanggar maka data tersebut akan dipindahkan ke tempat childnya (Down-Heap).

Trie

Trie adalah data structure yang efisien pada bidang re Trieval data. Bentuk trie sendiri berupa tree yang tiap nodenya di isi dengan karakter.

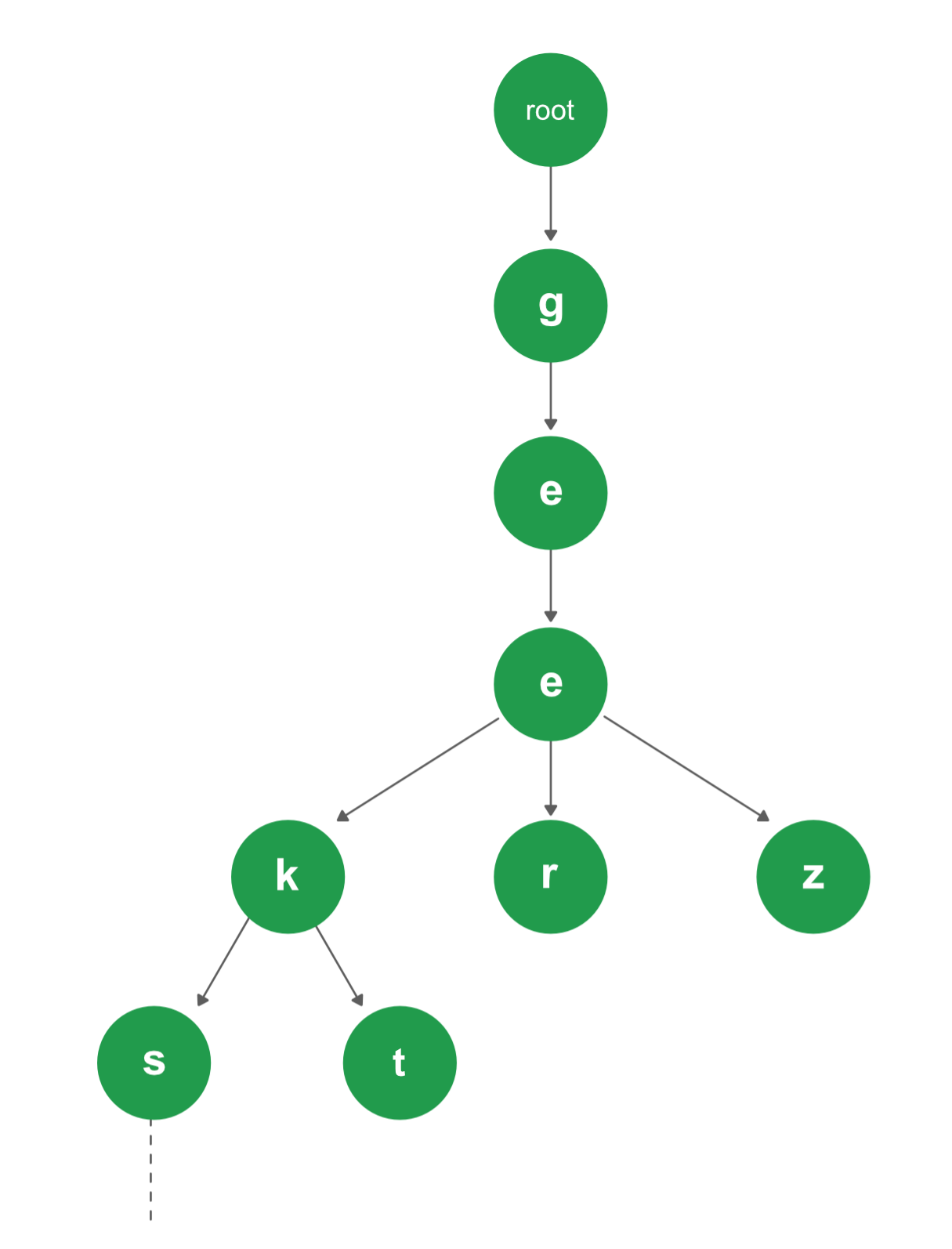Trie

Root pada Trie dapat dikosongkan ataupun di isi dengan karakter. Lalu kegunaan trie salah satunya adalah pada searching.

Referensi:

https://www.geeksforgeeks.org/heap-data-structure/

https://www.geeksforgeeks.org/binary-heap/

https://www.geeksforgeeks.org/trie-insert-and-search/

AVL Tree

AVL Tree
AVL Tree merupakan tipe binary tree yang dapat menyeimbangkan / self-balancing dirinya sendiri dimana perbedaan tinggi / height dari subtrees kiri dan kanan tidak boleh lebih dari satu untuk semua nodes. Kegunaan dari AVL Tree adalah mempercepat dan membuat operasi BST lebih efisien.

Contoh A

Gambar tree Contoh A diatas merupakan AVL Tree karena perbedaan tingginya hanya 1.

Contoh B

Gambar tree Contoh B dibawah bukanlah merupakan AVL Tree karena perbedaan tingginya lebih dari satu.

AVL Tree Insertion [Rotations]

Rotasi / Rotations AVL Tree dapat dibagi menjadi dua jenis yakni,

a. Single Rotation

    Single Rotation dapat dibagi menjadi dua jenis yakni,

        Single Left Rotation [LL Rotation]

        Single Right Rotation [RR Rotation]

b. Double Rotation

    Double Rotation dapat dibagi menjadi dua jenis yakni,

        Left Right Rotation [LR Rotation]

        Right Left Rotation [RL Rotation]

Penjelasan

Single Rotation

Jika treenya menjadi unbalanced, saat sebuah node di insert ke kanan subtree dari subtree kanan maka kita melakukan single left rotation.

LL Rotation

Sebaliknya jika kondisinya di kiri, maka kita melakukan single right rotation.

RR Rotation

Double Rotation

Left Right rotation adalah kombinasi dari left rotation lalu diikuti dengan right rotation, agar lebih dapat dipahami dapat dilihat dari gambar di bawah.

Sebuah node telah diinsert ke subtree kanan dari subtree kiri,
hal ini membuat tree menjadi tidak balance.

Pertama, kita melakukan left rotation di subtree kiri C,
hal ini membuat A menjadi subtree kiri dari B.

Lalu kita melakukan right rotation kepada treenya,
hal ini membuat B menjadi root baru dari tree dan C menjadi subtree kanan dari B.

Untuk Right Left Rotation dilakukan jika kondisinya kebalikannya.

            

    

Deletion

Deletion pada AVL Tree sama dengan Deletion pada BST, tetapi Deletion pada AVL Tree dapat menyebabkan ketidakseimbangan / unbalance pada tree. Untuk membuat AVL Tree tetap AVL Tree setelah deletion maka diperlukannya penyeimbangan ulang / re-balancing pada tree.

References:

https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm

https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

https://www.geeksforgeeks.org/avl-tree-set-2-deletion/

https://binusmaya.binus.ac.id/newStudent/#/class/resources.COMP6048/010544/1920/LEC/12104