Andrew Dharma Saputra
2301853823
2301853823
Hari: Selasa, 09/06/2020
Kelas: CB01-CL
Lecturer: Ferdinand Ariandy Luwinda ( D4522 ) dan Henry Chong ( D4460 )
AVL Tree
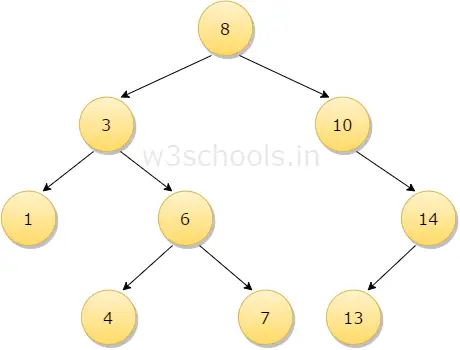
AVL Tree merupakan tipe binary tree yang dapat menyeimbangkan / self-balancing dirinya sendiri dimana perbedaan tinggi / height dari subtrees kiri dan kanan tidak boleh lebih dari satu untuk semua nodes. Kegunaan dari AVL Tree adalah mempercepat dan membuat operasi BST lebih efisien. |
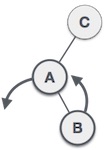
| Contoh A |
 |
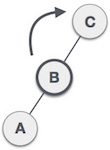
| Contoh B |
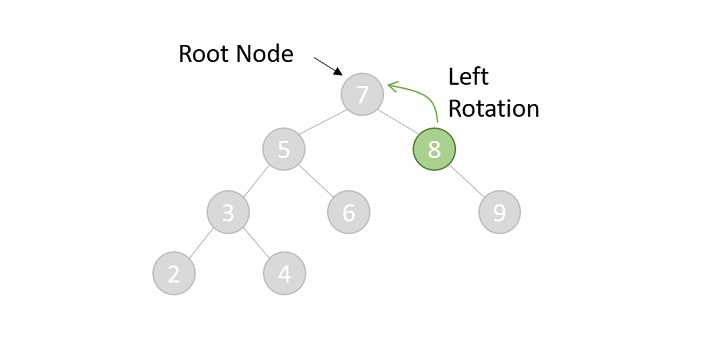
AVL Tree Insertion [Rotations]
Rotasi / Rotations AVL Tree dapat dibagi menjadi dua jenis yakni,
a. Single Rotation
Single Rotation dapat dibagi menjadi dua jenis yakni,
Single Left Rotation [LL Rotation]
Single Right Rotation [RR Rotation]
b. Double Rotation
Double Rotation dapat dibagi menjadi dua jenis yakni,
Left Right Rotation [LR Rotation]
Right Left Rotation [RL Rotation]
Penjelasan
Single Rotation
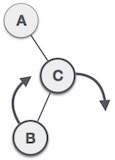
Jika treenya menjadi unbalanced, saat sebuah node di insert ke kanan subtree dari subtree kanan maka kita melakukan single left rotation.
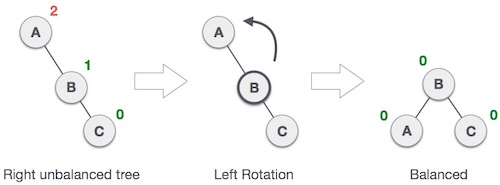 |
| LL Rotation |
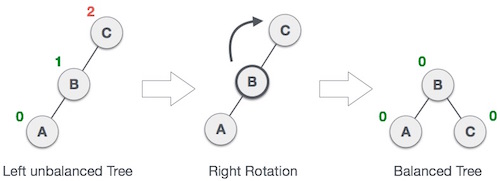 |
| RR Rotation |
Double Rotation
Left Right rotation adalah kombinasi dari left rotation lalu diikuti dengan right rotation, agar lebih dapat dipahami dapat dilihat dari gambar di bawah.
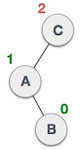 | ||||
| Sebuah node telah diinsert ke subtree kanan dari subtree kiri, hal ini membuat tree menjadi tidak balance.
|
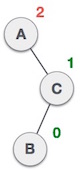
Deletion
Deletion pada AVL Tree sama dengan Deletion pada BST, tetapi Deletion pada AVL Tree dapat menyebabkan ketidakseimbangan / unbalance pada tree. Untuk membuat AVL Tree tetap AVL Tree setelah deletion maka diperlukannya penyeimbangan ulang / re-balancing pada tree.
Biasanya Heap dibagi menjadi dua yakni,
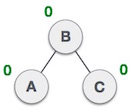
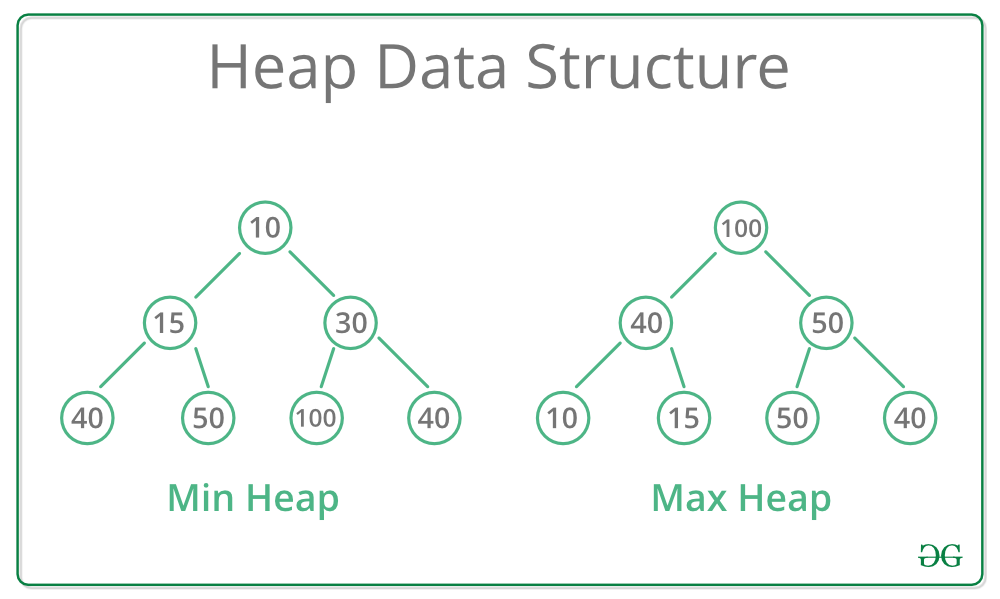
Pada Max-Heap key pada root harus lebih besar daripada key semua childnya. Begitu juga untuk childrennya yang menjadi parent harus lebih besar daripada childrennya.
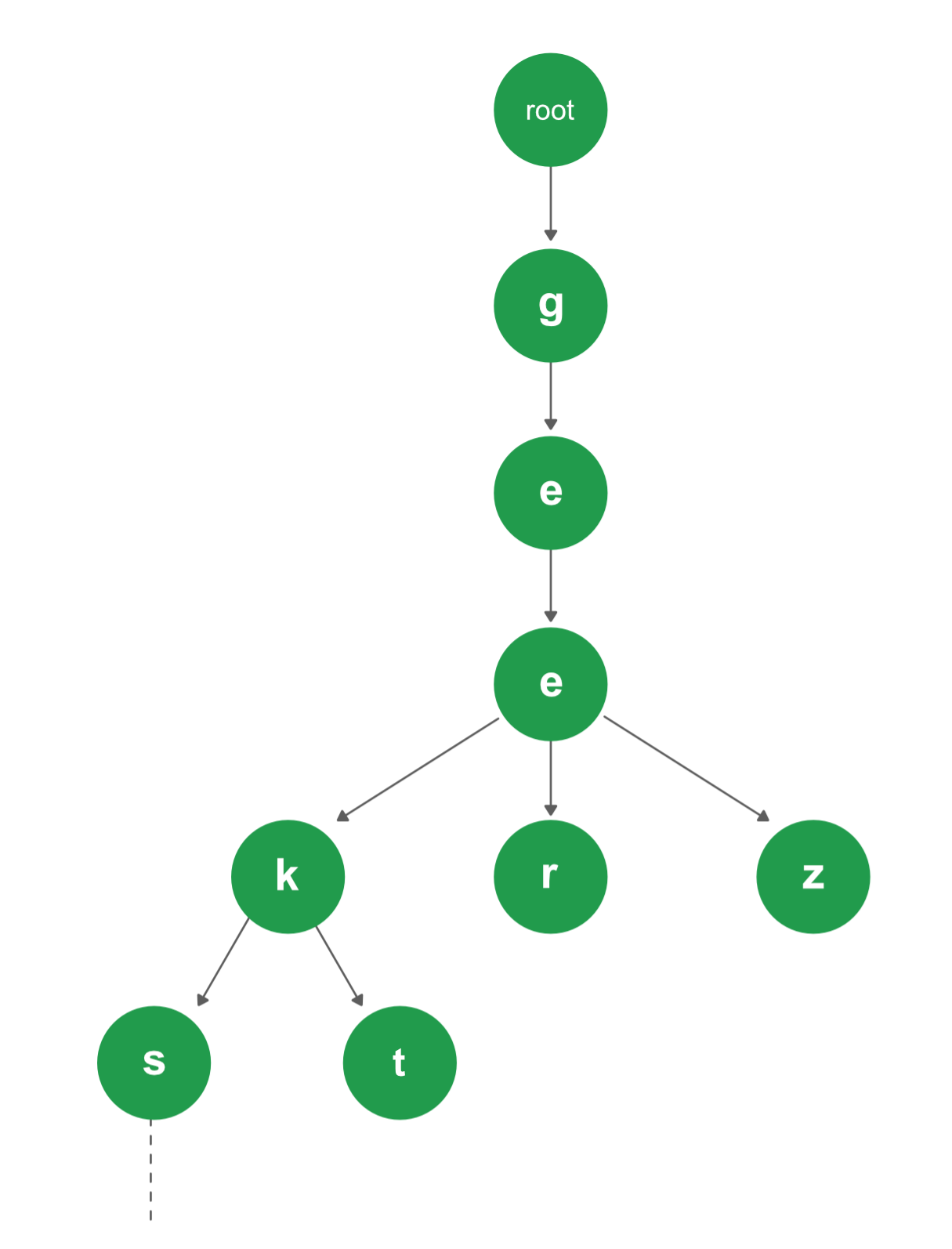
Root pada Trie dapat dikosongkan ataupun di isi dengan karakter. Lalu kegunaan trie salah satunya adalah pada searching.
Heap
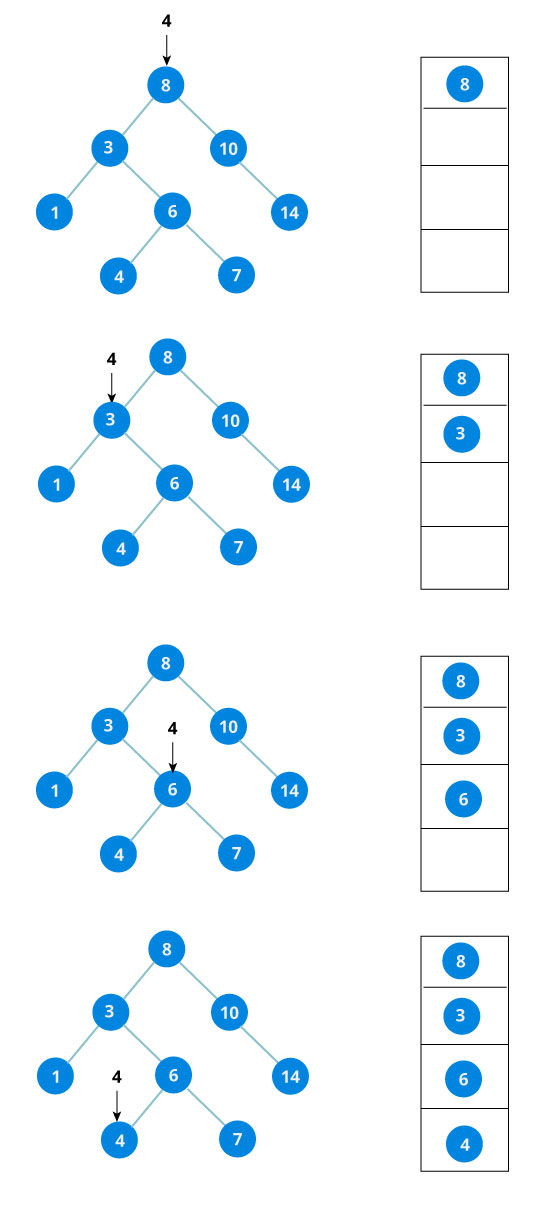
Heap adalah data structure yang spesial dimana ia tree-based yang treenya adalah complete binary tree.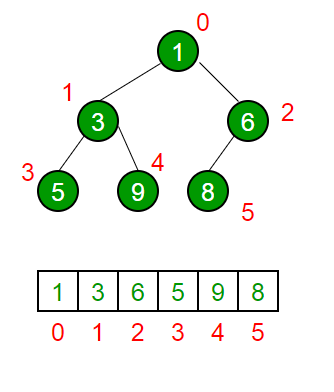 |
| Array to Heap |
Max-Heap dan Min-Heap
 |
| Min & Max |
Pada Min-Heap key pada root harus lebih kecil daripada key semua childnya. Begitu juga untuk childrennya yang menjadi parent harus lebih kecil daripada childrennya.
Insertion
Saat kita meng-insert data, data akan dimasukan di index terakhir pada array heap tersebut lalu data akan dibandingkan dengan parentnya, jika kondisi Min/Max Heap dilanggar maka data tersebut akan dipindahkan ke tempat parentnya (Up-Heap).
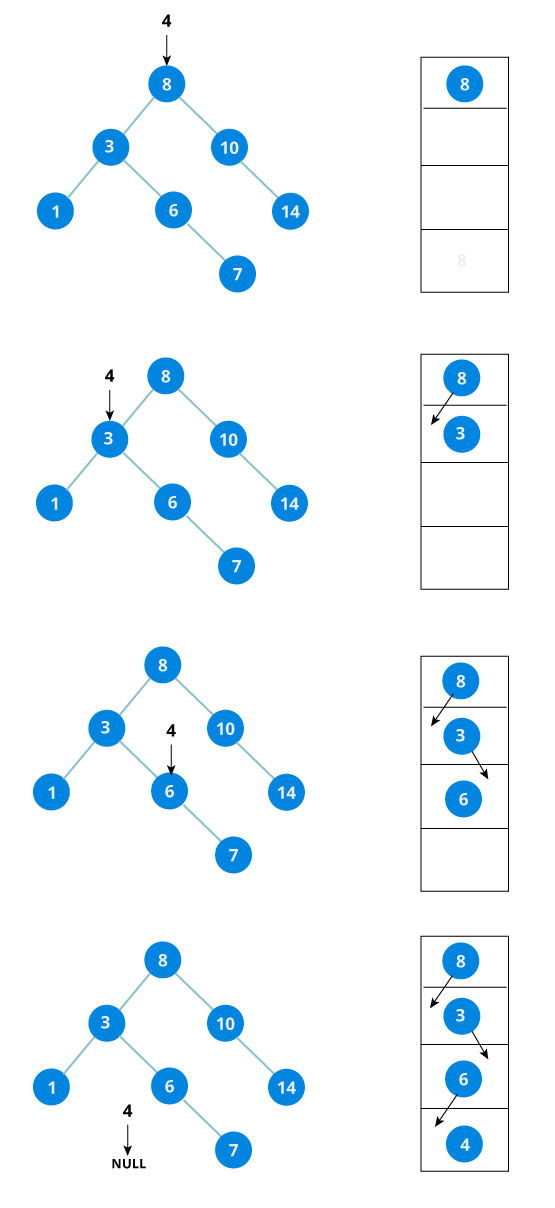
Deletion
Saat kita meng-delete data pada heap, maka root dari heap akan terhapus, lalu array heap terakhir akan langsung menggantikan root yang terdelete. Lalu data tersebut akan di bandingkan dengan childnya, jika kondisi Min/Max Heap dilanggar maka data tersebut akan dipindahkan ke tempat childnya (Down-Heap).
Trie
Trie adalah data structure yang efisien pada bidang re Trieval data. Bentuk trie sendiri berupa tree yang tiap nodenya di isi dengan karakter.
 |
| Trie |