Binary Search Tree

Binary Search Tree
Binary Search Tree (BST)
Binary search tree adalah sebuah binary tree data structure yang berlandaskan node.
Binary search tree memiliki keuntungan yakni searching dan sortingnya cepat, dan juga deletion dan insertionnya mudah.
Binary search tree memiliki beberapa sifat yakni:
1. Anak pada bagian kiri dari node x lebih kecil daripada x.
2. Anak pada bagian kanan dari node x lebih besar daripada x.
3. Anak dari node x juga termasuk binary search tree.

Pada gambar diatas kita dapat lihat bahwa 8 adalah root (akar),
angka 8 tersebut memiliki anak 3 dan 10,
karena 3 < 8 maka dia diletakan di sebelah kiri,
karena 10 > 8 maka dia diletakan di sebelah kanan,
siklus terus berlanjut sampai anak terakhir,
anak terakhir tersebut (1, 4, 7, 13) disebut daun.

Binary search tree memiliki 3 operation basic yakni:
- Searching
- Insertion
- Deletion

BST Search
Misalkan ingin mencari angka 4 dari binary search tree di bawah.
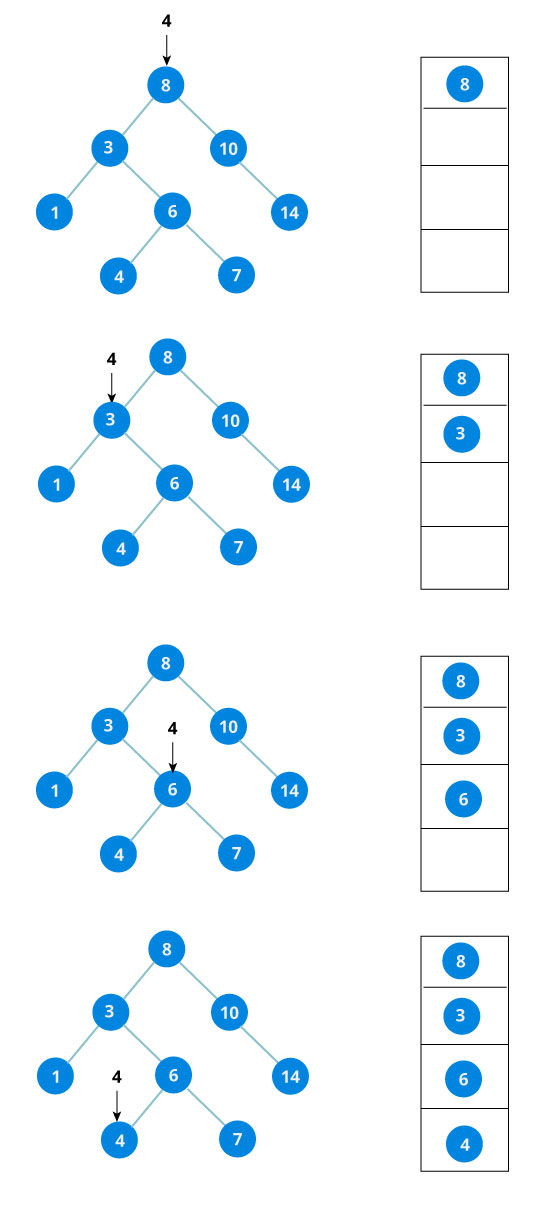
Misalkan x adalah posisi kita,
pencarian dimulai dari root yakni 8,
karena 8 != 4 dan 8 > 4 maka,
x akan pindah ke kiri (3),
karena 3 != 4 dan 3 < 4 maka,
x akan pindah ke kanan (6),
karena 6 != 4 dan 6 > 4 maka,
x akan pindah ke kiri (4),
karena 4 == 4 maka searching selesai.

BST Insertion
Misalkan kita ingin memasukan angka 4 ke dalam binary search tree di bawah.

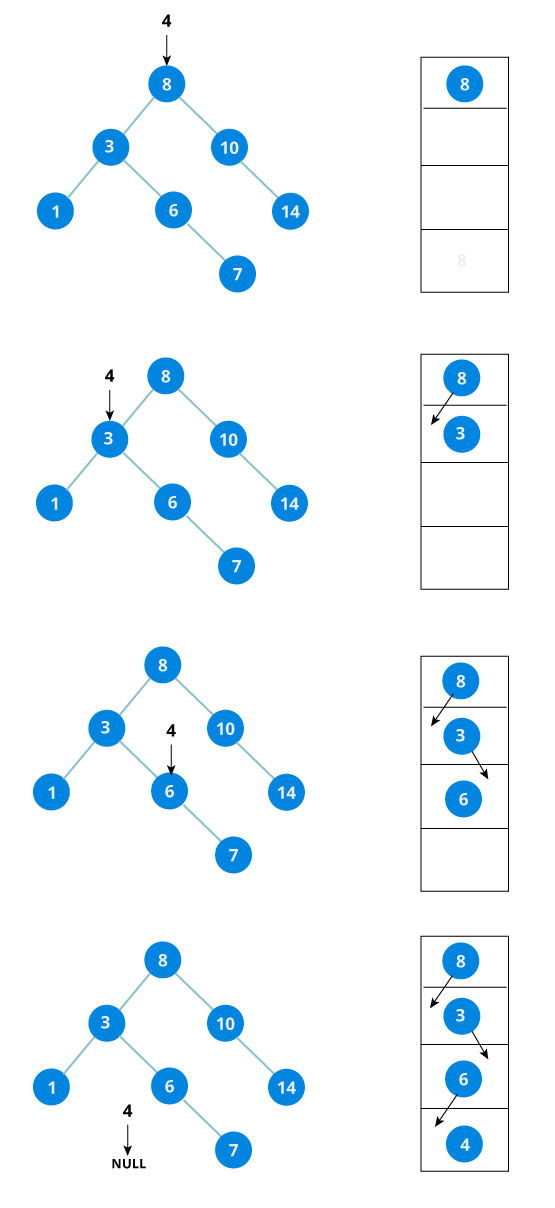
Misalkan x adalah posisi kita,
pencarian dimulai dari root yakni 8,
karena 8 > 4 maka,
x pindah ke kiri (3),
karena 3 < 4 maka,
x pindah ke kanan (6),
karena 6 > 4 maka,
x pindah ke kiri,
karena x == null maka,
4 di masukan ke x.

BST Deletion
Deletion pada BST dapat dibagi menjadi 3 kasus.

Kasus 1:
Misalkan kita ingin menghapus angka -4 dari dalam binary search tree di bawah kiri.

Karena -4 tidak memiliki anak maka ia dapat dihapus (seperti gambar di atas kanan).

Kasus 2:
Misalkan kita ingin menghapus angka 18 dari dalam binary search tree di bawah ini.

Karena 18 memiliki hanya satu anak maka,

angka 18 akan dihapus dan parent dari 18 akan disambungkan ke anak dari 18.


Kasus 3:
Misalkan kita ingin menghapus angka 12 dari dalam binary search tree di bawah ini.

Misalkan x berada pada angka 12.
Karena 9 tidak ada anak maka akan di cek ke kanan,
karena 19 < 21 dan 19 > 9 maka 19 akan dipilih sebagai pengganti 12,
kita tidak dapat pakai 25 karena 25 > 21.

Referensi:
https://www.programiz.com/dsa/binary-search-tree
https://www.geeksforgeeks.org/binary-search-tree-data-structure/
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/

http://www.algolist.net/Data_structures/Binary_search_tree/Removal